We are given the following function:
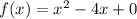
We are asked to determine the average rate of change in the interval:
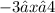
To do that we will use the following formula:
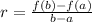
Where "a" and "b" are the extreme points of the interval.
Now, we substitute the value of "x = -3" in the function:
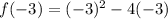
Solving the operations:
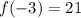
Now, we substitute "x =4":
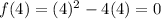
Now, we substitute the values in the rate of change:
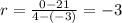
Therefore, the rate of change is -3.