Question

A. Use substitution to solve for two values of yB. Using the values of y you just found, find the coordinates of the points of intersection of these two shapes. Write answers in (x,y) form

Answer 1

Step 1: Write the two equations

`\begin{gathered} x^2+y^2\text{ - 16y + 39 = 0 ----------- (1)} \\ y^2-x^2\text{ - 9 = 0 --------------- (2)} \end{gathered}`

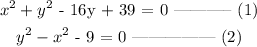
Step 2: Make x square the subject of the formula from equation 2.

`\begin{gathered} y^2-x^2\text{ - 9 = 0} \\ y^2-9=x^2 \end{gathered}`

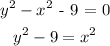
Step 3: Substitute x square in equation 1

`\begin{gathered} \text{Equation 1: x}^2+y^2\text{ - 16y + 39 = 0} \\ y^2-9+y^2\text{ - 16y + 39 = 0} \\ \text{Add similar terms} \\ 2y^2\text{ - 16y + 30 = 0} \\ \text{Divide through by 2} \\ y^2\text{ - 8y + 15 = 0} \end{gathered}`

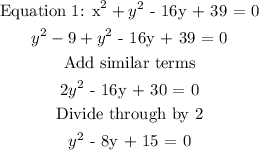
Step 4: Use the factorization method to solve for y.

`\begin{gathered} y^2\text{ - 8y + 15 = 0} \\ To\text{ factorize, choose two number when added will give -8 and} \\ \text{when multiply will give +15.} \\ \text{The two intergers are -3 and -5.} \end{gathered}`

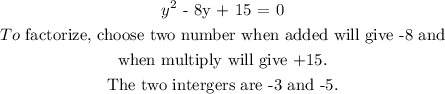
Step 5: Split -8y into -3y and -5y

`\begin{gathered} y^2\text{ - 3y - 5y + 15 = 0} \\ \text{Pair two terms and factor out common factor.} \\ y(y\text{ - 3) - 5(y - 3) = 0} \\ (y\text{ - 3)(y - 5) = 0} \\ y\text{ - 3 = 0 or y - 5 = 0} \\ y\text{ = 3 or 5} \end{gathered}`

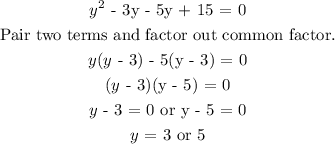
Step 6: Find the corresponding values of x, by substituting y in any equation.

Substitute y in equation 2.

`\begin{gathered} \text{Equation 2: y}^2-9=x^2 \\ \text{for y = 3} \\ 3^2-9=x^2 \\ 9-9=x^2 \\ x^2\text{ = 0} \\ \text{x = }\sqrt[]{0} \\ \text{x = 0} \\ \text{for x = 5} \\ 5^2-9=x^2 \\ 25-9=x^2 \\ 16=x^2 \\ x\text{ = }\sqrt[]{16} \\ x\text{ = }\pm\text{4} \end{gathered}`

Step 7: Final answer

Coordinates of the point of intersection are:

(0,3) , (4, 5) and (-4, 5)