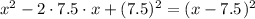A perfect square trinomial has the following structure:
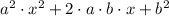
We were given the expression:
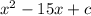
By comparing both expressions we know that:
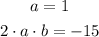
We can replace the value of a on the second expression to find b.
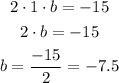
The value of c is:
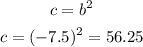
Therefore the perfect square trinomial is:
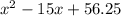
It can be written as the following binomial squared: