Question

If the polynomial function is written in the form P(x) = c(x − a)2(x − b)(x + d), where a, b, c, and d are all positive integers, then what is the value of a?

Answer 1

`P(x)=c(x-a)^2(x-b)(x+d)`

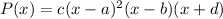
Since the leading coeficient is 1, then c must be equal to 1.

Now, by looking at the graph, we have that

`\begin{gathered} P(-3)\text{ = 0} \\ P(1)\text{ = 0} \\ P(4)\text{ = 0,} \end{gathered}`

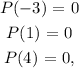
so, we have that (x+3), (x-1) and (x-4) are all factors, and so we have that d=3.

We only need to figure out if a=1 or a=4.

So we have two options

`\begin{gathered} P_1(x)=(x-1)^2(x-4)(x+3) \\ or \\ P_2(x)=(x-4)^2(x-1)(x+3) \end{gathered}`

If we evaluate the polynomial in x=--2 and x=3 then it have to be negative, so

`\begin{gathered} P_1(-2)=(-2-1)^2(-2-4)(-2+3)=9(-6)(1)\text{ = -36} \\ \text{and} \\ P_1(3)=(3-1)^3(3-4)(3+3)=4(-1)(6)=-24. \end{gathered}`

on the other hand

`\begin{gathered} P_2(-2)=(-2-4)^2(-2-1)(-2+3)=36(-3)(1)\text{ = -108} \\ \text{and} \\ P_2(3)=(3-4)^2(3-1)(3+3)=1(2)(6)=12 \end{gathered}`

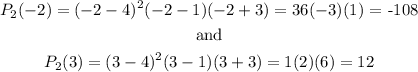
We can see that the last evaluation is not negative, so this polynomial (P2) cannot be the one we are looking for. Thus, the polynomial is

`P(x)=(x-1)^2(x-4)(x+3)`

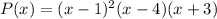
and a=1.