Explanations:
a) Given the equation of a curve expressed as:
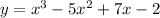
On differentiating the function, we will have:
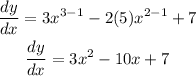
If the dy/dx = 0, then the x-ccordinates will be:
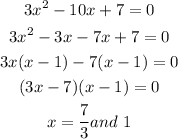
Determine the turning points
If x = 7/3 then;
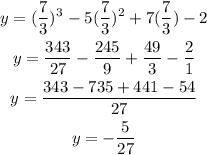
One of the turning points is (7/3, -5/27)
if x = 1 then;
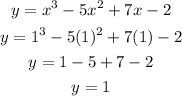
The other turning point is at (1, 1)
b) To get the minimum and maximum point, we will find the second derivative of the function as shown:
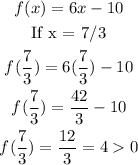
Since f''(x) > 0 at the point where x = 7/3, hence the turning point (7/3, -5/27) is at the minimum
At the point where x = 1,
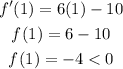
Since f''(x) > 0 at the point where x = 1, hence the turning point (1, 1) is at the maximum point.
c) To sketch the turning points (1, 1), and (7/3, -5/27)
To get other points, at x = 2
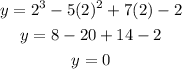
Another coordinate point will be at (2, 0)