Solution:
Given the data below:

1) The range is the spread of data from the lowest to the highest value in the distribution.
In other words,

In this case,
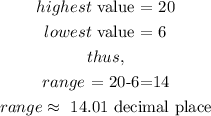
Thus, the range is 14.0 (1 decimal place)
2) Population variance:
The population variance is expressed as

Thus, we have
![\begin{gathered} ((14-12.8)^2+(12-12.8)^2+(18-12.8)^2+(10-12.8)^2+(8-12.8)^2+(6-12.8)^2+(15-12.8)^2+(9-12.8)^2+(16-12.8)^2+(20-12.8)^2)/(10) \\ =(187.6)/(10) \\ =18.76 \\ population\text{ variance}\approx18.8\text{ \lparen1 decimal place\rparen} \end{gathered}]()
Thus, the population variance is 18.8 (1 decimal place)
3) Standard deviation:
the standrard deviation is the square root of the variance.
Hence, we have
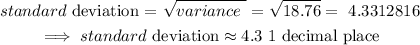
Hence, the standard deviation is 4.3 (1 decimal place)