We are given that a car decelerates from 29 m/s to 15.8 m/s in 6.37 seconds. To determine the force that causes de deceleration we will use Newton's second law:
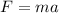
Where:
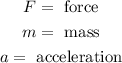
We are given the mass therefore we need to determine the acceleration. To do that we will use the following equation of motion:
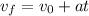
Where:
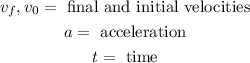
Now, we solve for the acceleration. First, by subtracting the initial velocity from both sides:
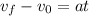
Now, we divide both sides by "t":
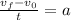
Now, we plug in the given values of velocity and time:
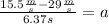
Solving the operations:
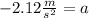
Now, we use this value together with the mass to determine the force:
![F=(1370\operatorname{kg})(-2.12(m)/(s^2))]()
Solving the product:
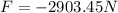
Therefore, the magnitude of the force is 2903.45 Newtons.