So we must solve this by using a proportion. This means that we will have to solve an equation like this:

So, we know that the price per pund of cherries is constant. This is given by the total cost of a certain amount of pounds of cherries divided by the number of pounds. So the price per pound for her normal recipe is given by:
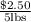
If she needs to double the recipe then she must purchase 10 pounds. If we use x for how much she'll have to pay for these 10 pouns we get that the price per pound of cherries is:
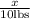
If we equalize both expressions for the price per pound of cherries we'll have the proportion equation like the one I stated before:
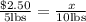
If we multiply both sides by 10lbs:
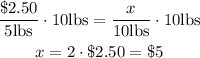
Then the answer is x=$5.