We are given a graph of a relationship between total price (p) and time (d)
Since the graph seems to be linear, the general form of such a graph is given by
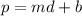
Where m is the slope and b is the y-intercept.
The y-intercept is the point where the line intersects the y-axis.
From the graph, we see that the line intersects the y-axis at 30
So, the y-intercept is 30
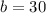
The slope of the line is given by
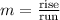
The rise is the vertical distance between the two points on the line.
The run is the horizontal distance between the two points on the line.
As you can see, we selected two points on the graph. ( you may select any other)
The rise is 40 and the run is 2, so the slope is
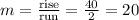
So, the slope of the line is 20
Therefore, the equation of the line becomes
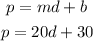
Option D is the correct answer.