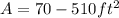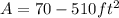
1) Note that this is a rectangle, so we can use the formula for the Area of a rectangle. So let's write it out and then plug into that the given measures:
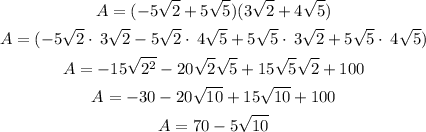
We can simplify those square roots and combine the terms with the same radical. So we can tell the area is: