C and E
1) Let's evaluate that so we can find out the answers:
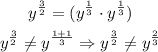
So Student 1 has come to a false conclusion.
• Student 2
![\begin{gathered} y^{(3)/(2)}=(y\cdot y\cdot y)^{(1)/(2)}\Rightarrow y^{(3)/(2)}=(y^3)^{(1)/(2)}\Rightarrow y^{(3)/(2)}=y^{(3)/(2)} \\ (\sqrt[]{y\cdot y\cdot y})=(y^{(3)/(2)})=(\sqrt[]{y^3}) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/59djuyvrsfy79q05lri90peuc9iuwj6ki7.png)
Note that we can add the exponents of a product of power with the same exponent. Also, rational exponents indicate a radical.
So Student 2 has come to a True conclusion
• Student 3
![\begin{gathered} y^{(3)/(2)}=(y^{(1)/(2)+(1)/(2)+(1)/(2)})\Rightarrow y^{(3)/(2)}=y^{(3)/(2)} \\ (\sqrt[]{y}\cdot\sqrt[]{y}\cdot\sqrt[]{y})=(\sqrt[]{y}^3)\text{ =}y^{(3*1)/(2)}=y^{(3)/(2)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/k0gxm18t66nvsprdc6x0nrasfb58ooxx2s.png)
Since by the exponents' property the sum of the exponents within a product of same base powers and rational exponents rewritten as radicals, we can state that Studen t 3 has come up to a true conclusion.
3) Hence, the answers are:
C and E