Question

A store sells tents, sleeping bags, and camp stools. A customer buys a tent, 3 sleeping bags, and 2 camp stools for $175. The price of the tent is6 times the cost of a camp stool. The cost of a sleeping bag is $40 more than the cost of a camp stool. Find the cost of each item.

Answer 1

Let x be cost of a tent, y be cost of a bag and z be cost of a camp stool.

The cost of a tent, 3 sleeping bags and 2 camp stools is $175. So equation is,

`x+3y+2z=175`

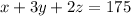
The price of the tent is 6 times the cost of a camp stool. So equation is,

`x=6z`

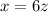
The cost of sleeping bag is $40 more than the camp stool cost. So equation is,

`y=40+z`

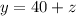
Substitute the value of x and y in equation x + 3y + 2z = 175 and solve for z.

`\begin{gathered} 6z+3\cdot(40+z)+2z=175 \\ 6z+120+3z+2z=175 \\ 11z=175-120 \\ z=(55)/(11) \\ =5 \end{gathered}`

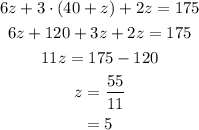
Substitute the value of z in equation y = 40 + z and equation x = 6z to determine the value of y and z respectively.

`\begin{gathered} y=40+5 \\ =45 \end{gathered}`
`\begin{gathered} x=6\cdot5 \\ =30 \end{gathered}`

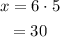
So cost of a tent is 30, cost of a sleeping bag is 45 and cost of a camp stool is 5.