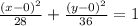As given by the question
There are given that the vertices and focii point is:
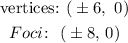
Now,
From the general form of the equation of hyperbola:
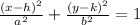
Then,
Firs find the center (h, k) of the hyperbola:
So
We know that the center of hyperbola must be at the midpoint of the given foci:
Then,
The point of foci is:
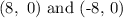
So,
The center of the hyperbola is:
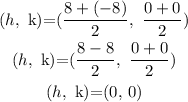
Now,
Find a which equals half the length of the vertical major axis.
The distance of any focus of the hyperbola from the center is denoted c
So,
The distance of focus (8, 0) and the center (0,0) is:
![\begin{gathered} c=\sqrt[]{(0-8)^2+(0-0)^2} \\ c=\sqrt[]{(8)^2+(0)^2} \\ c=\sqrt[]{64+0} \\ c=\sqrt[]{64} \\ c=8 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6d4eog3fcumclbrmib50bmfsok81hj2k6d.png)
Now,
The distance of any vertex of the hyperbola from the center is denoted a
So,
The vertex point is:

Then,
![\begin{gathered} b=\sqrt[]{(0-6)^2+(0-0)^2} \\ b=\sqrt[]{36} \\ b=6 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6gyizcpdrwucs9vb2vg9k5npp8t90zufxm.png)
And,
Find a which equals half the length of the horizontal minor axis and we know that the relationship between c, a and b.
So,
From the formula of retaionship between c, a and b.
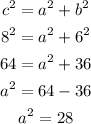
Then,
From the standard form of the hyperbola:
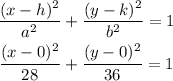
Hence, the standard form of the hyperbola is shown below: