Question

21)A total of $36,000 is invested in two corporate bonds that pay 10% and 12.5% simple interest. The annual interest earned is $3,918.75a) Write a system of equations that describes the situation.b) Determine the amount of each investment.

Answer 1

Part A

We need to write a system of equations describing the investment of $36,000 in two corporate bonds that pay 10% and 12.5% simple interest.

Let's call x the amount, in dollars, invested with 10% simple interest, and y the amount, in dollars, invested with 12.5% simple interest.

We have:

`x+y=36000`

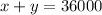
Also, 10% applied on x plus 12.5% applied on y resulted in 3918.75 dollars. So, we have:

`\begin{gathered} 10\%\cdot x+12.5\%\cdot y=3918.75 \\ \\ 0.1x+0.125y=3918.75 \end{gathered}`

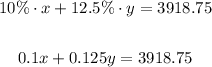
Therefore, the system of equations is:

Answer

`\begin{gathered} x+y=36000 \\ \\ 0.1x+0.125y=3918.75 \end{gathered}`

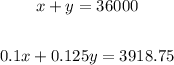
Part B

We need to solve for x and y.

From the first equation, we obtain:

`y=36000-x`

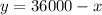
Now, using this in the second equation, we obtain:

`\begin{gathered} 0.1x+0.125(36000-x)=3918.75 \\ \\ 0.1x+4500-0.125x=3918.75 \\ \\ -0.025x+4500=3918.75 \\ \\ -0.025x=3918.75-4500 \\ \\ -0.025x=-581.25 \\ \\ x=(-581.25)/(-0.025) \\ \\ x=23250 \end{gathered}`

Then, y is given by:

`\begin{gathered} y=36000-23250 \\ \\ y=12750 \end{gathered}`

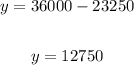
Answer:

$23250 at 10%

$12750 at 12.5%