We are told that the interest is compounded continuously, therefore, we use the following formula:
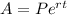
Where "A" is the present value, "P" the initial value, "r" the interest rate, and "t" the time:
Now we solve for "r", first by dividing both sides by "P":
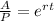
Now we take natural logarithm to both sides:
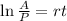
Now we divide both sides by "t":
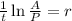
Now we replace the given values:
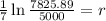
Solving the operations we get:
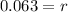
Therefore, the interest rate is 6.3%.