Question

A particular fruit's weights are normally distributed, with a mean of 601 grams and a standard deviation of 12 grams.If you pick one fruit at random, what is the probability that it will weigh between 618 grams and 624 gramsRound to 3 decimal places.

Answer 1

Given:

population mean = 601 grams

population standard deviation = 12 grams

Find: the probability of picking a fruit that has a weight between 618 grams and 624 grams

Solution:

To get the probability of one object, we use the formula below.

`z=(x-\mu)/(\sigma)`

where x = weight of an object, μ = population mean, and σ = standard deviation, and z = equivalent z-value of the weight.

Let's start with the first boundary of the weight at 618 grams.

1. Subtract the population mean from the 618 grams. Divide the result by the population standard deviation.

`618-601=17`
`17/12\approx1.417`

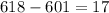
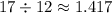
The equivalent z- value of 618 grams is approximately 1.417.

Let's now calculate the equivalent z-value of the other boundary at 624 grams. Apply the same steps above.

`624-601=23`
`23/12\approx1.917`

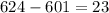
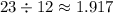
The equivalent z- value of 624 grams is approximately 1.917.

Let's graph these z-values under the normal curve and shade the area between them.

To determine the probability, we have to find the area in the shaded region because that indicates the area between 618 grams and 624 grams.

To find the area, refer to the standard normal distribution table.

Based on the table, the area from the center to z = 1.917 is 0.4724 while the area from the center to z = 1.417 is 0.4217.

To determine the area between the two z-values, let's subtract 0.4217 from 0.4724.

`0.4724-0.4217=0.0507\approx0.051`

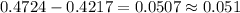
The area between the z-values 1.417 and 1.917 is approximately 0.051.

Hence, the probability that a random fruit weighs between 618 and 624 grams is approximately 0.051.