Given:
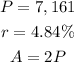
To Determine: How long it will take the fund to be worth double the amount
Solution
The formula for finding the amount for a compound interest is given as

Substitute the given into the formula
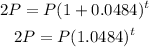
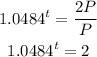
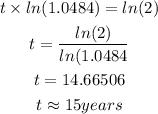
Hence, the time it will the investment to be doubled is 15 years