If the two lines are perpendicular then the products of thier slope is ( -1 )
The general form of equation of line :
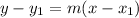
where, m = slope, (x1, y1) are the passing point
The given equation of line : 2x - 7y = -6
Simplify in the general form
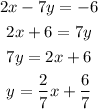
On comparing with the general form of line, we get slope = 2/7
Let the slope of the perpendicular line is m
Thus, from the slope creteria of perpendicular line : m(2/7)=-1
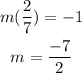
Substitute the passing point(-2,6) and slope m = -7/2 in the equation of line.
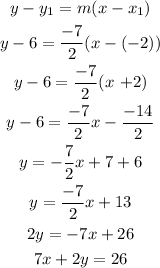
Equation of perpendicular line is 7x + 2y = 26
Answer : 7x + 2y = 26