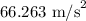Question

D. O 145.451 NE. 89.649 N11. An object of mass 3.123 kg is being pulled by ahorizontal force of 210 N on a horizontal force.The coefficient of kinetic friction betweenthe object and the surface is 0.1. Calculate theacceleration of the object. (1 point)A. O 30.373 m/s ²B. O 66.263 m/s²C. O 122.405 m/s²110.843 m/s2D.E.88.439 m/s²

Answer 1

Given:

The mass of the object is,

`m=3.123\text{ kg}`

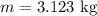
The object is being pulled by the force,

`F=210\text{ N}`

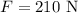
The coefficient of kinetic friction between the object and the surface is

`\mu=0.1`

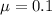
To find:

The acceleration of the object

Step-by-step explanation:

The frictional force on the object is,

`\begin{gathered} f=\mu mg \\ =0.1*3.123*9.8 \\ =3.06\text{ N} \end{gathered}`

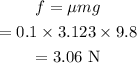
The resultant force on the object is,

`\begin{gathered} F_(net)=F-f \\ =210-3.06 \\ =206.94\text{ N} \end{gathered}`

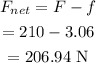
The acceleration of the object is,

`\begin{gathered} a=(F_(net))/(m) \\ =(206.94)/(3.123) \\ =66.263\text{ m/s}^2 \end{gathered}`

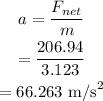
Hence, the acceleration of the object is,

`66.263\text{ m/s}^2`