To determine wheter the graph could ne a polynomial function you have to take into account that graphs of polynomial functions of degree 2 or more don't have sharp corners and also have no breaks.
Thus, this could be a polynomial function.
To list the real zeros, you have to identify at which points the function crosses the x-axis. Then, it is at x=-3, x=0 and x=2. These are the real zeros of the function.
To state the least degree, given a polynomial function has degree n:
- The function has at most n x-intercepts
- The function has at most (n-1) turns.
Given the first condition, the graph has 3 x-intercepts (this could be the degree) but also given the second condition, the graph has 2 turns, then:
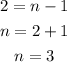
Thus, the polynomial function has a least possible degree of 3