The question to simplify is:
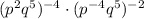
We can use the power property of exponents to simplify this further. The power property is >>>
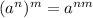
Simplifying, we get:
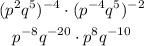
When we have two same bases multiplied, we add the exponents. So, let's simplify the exponents of "p" and "q":
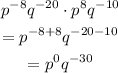
We know anything to the power 0 is "1". So, we have:
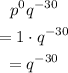
To make the exponent positive, we take the variable to the denominator, so it becomes >>>
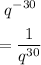
**The first answer choice is right**