Question

What inequality does the graph represent?A) 14x + 7y > 21 B) 14x + 7y < 21 C) 14x + 7y < 21 D) 14x + 7y > 21

Answer 1

Let's first identify at least two points that pass through the line and generate an equation. We've identified two points at A(x1,y1) = (0,3) and B(x2,y2) = (1,1).

Let's generate the equation by getting the value of the slope (m) and y-intercept (b) then substitute it to the Slope-Intercept Formula.

`\text{ m = }\frac{y_2-y_1}{x_2-x_1_{}}\text{ = }\frac{1\text{ -3}}{1\text{ -0}}\text{ = }(-2)/(1)=-2\text{ }`

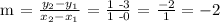
Let's determine the value of the y-intercept (b) at m = -2 and (x,y) = (0,3).

`\text{ y = mx + b }\rightarrow\text{ 3 = (-2)(0) + b }\rightarrow\text{ b = 3}`

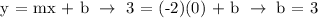
Therefore, the formula of the line is:

`\text{ y = mx + b }\rightarrow\text{ y = (-2)x + 3}`
`\text{ y = -2x + 3 }\rightarrow\text{ 2x + y = 3}`

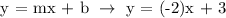
The shaded area is at the left side of the graph and the boundary is solid. Therefore, the inequality represented by the graph must be:

`\text{ 2x + y = 3 }\rightarrow\text{ 2x + y }\leq\text{ 3}`

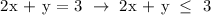
The given choices arent's their simplest form, it has an LCM of 7. Let's use this LCM to transform the inequality the same as the choices given. We get,

`\text{2x + y }\leq\text{ 3 }\rightarrow\text{ 7(2x + y }\leq\text{ 3)}`
`\text{ 14x + 7y }\leq21`

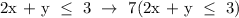
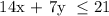
The answer is letter C.