In order to model this situation, let's use the following exponential equation:
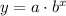
Since the initial population is 120, we have a = 120, and since the number of fish decreases by 1/4 each year, the value of b is 3/4.
So the equation is:
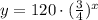
For x = 1, the value of y is equal to:
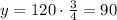
Looking for the graph with the points (0, 120) and (1, 90), we have the bottom left graph as the correct one.