Question

A 0.75 kg object is experiencing a net force of 25 N while traveling in a circle at avelocity of 28.6 m/s. What is the radius of its motion?

Answer 1

24.54 m

Step-by-step explanation:

The net force in a circular motion is equal to

`\begin{gathered} F_(net)=ma_c \\ F_(net)=m\cdot(v^2)/(r) \end{gathered}`

Where m is the mass, v is the velocity and r is the radus. Solving fror r, we get

`\begin{gathered} F_(net)\cdot r=m\cdot v^2 \\ \\ r=(m\cdot v^2)/(F_(net)) \end{gathered}`

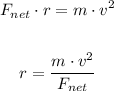
Now, we can replace m = 0.75 kg, v = 28.6 m/s and Fnet = 25 N to get

`\begin{gathered} r=\frac{0.75\text{ kg}\cdot(28.6\text{ m/s\rparen}^2}{25\text{ N}} \\ \\ r=24.54\text{ m} \end{gathered}`

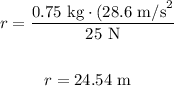
Therefore, the radius of te motion is 24.54 m