Rate of boat in still water is 45 m/h
Rate of current is 5 m/h
Step-by-step explanation
Step 1
let x represents the spped of the boat
let y represents the rate of the current
hence
A) going upstream
the current is opposite to the movement, so we need to subtract the rate of the current form the rate of the motor boat ,so
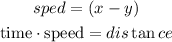
replace
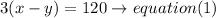
B) going downstream
we need to add the rates , so the rate is (x+y)
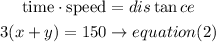
Step 2
solve the equations
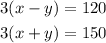
divide both side of equation(1) by 3
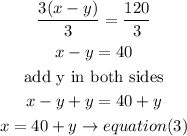
now, divide both sides of the equation (2) by 3 and replace the x value we got previously
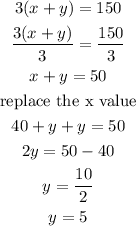
finally, replace the y value into equation (3) to know x
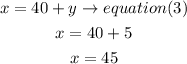
therefore.
Rate of boat in still water is 45 m/h
Rate of current is 5 m/h
I hope this helps you