1 Answer

Ask a Question

Nick Fortescue · Answer 1 · 2023-07-19T09:40:09+0000

Answer:

Option E is correct. 320K

Explanations:

In order to get the normal boiling point of the liquid, we will use the Clausius-Clapeyron equation expressed according to the equation:

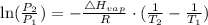
$\ln ((P_2)/(P_1)_{})=-(\triangle H_(vap))/(R)\cdot((1)/(T_2)-(1)/(T_1))$

where:

P1 is the vapor pressure of that substance at T1

P2 is the vapor pressure of that substance at T2

ΔHvap is the enthalpy of vaporization.

R is the gas constant - usually expressed as 8.314J/Kmol

Given the following parameters:

$\begin{gathered} P_1=102\operatorname{mm}Hg \\ P_2=760\operatorname{mm}Hg(cons\tan t) \\ T_1=273K \\ \triangle H_{\text{vap}}=30.8\text{kJ/mol} \\ R=8.31\text{J/Kmol} \end{gathered}$

Substitute the given parameters into the formula to get T2

$\ln (\frac{760_{}}{102_{}}_{})=-\frac{30.8*10^3(J)/(mol)_{}}{\frac{8.31J}{\operatorname{km}ol}}\cdot(\frac{1}{T_2_{}}-\frac{1}{273_{}})$

Simplify the result to get the value of T2

$\begin{gathered} \ln (7.4509)=-3,706.3778((1)/(T_2)-(1)/(273)) \\ 2.0083=(-3,706.3778)/(T_2)+13.5765 \\ (-3,706.3778)/(T_2)=2.0083-13.5765 \\ (-3,706.3778)/(T_2)=-11.5682 \\ -11.5682T_2=-3,706.3778 \\ T_2=(-3,706.3778)/(-11.5682) \\ T_2=320.39K \\ T_2\approx320K \end{gathered}$

Hence the normal boiling point of this liquid is approximately 320K

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

Answer:

Explanations:

0 Comments

Please log in or register to add a comment.

Other Questions