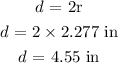Answer:
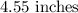
Step-by-step explanation:
Here, we want to get the diameter of one of the balls
Firstly, we need to get the size of one of the balls
We can get this by dividing the total volume of the three balls by 3
Mathematically, we have this as:

To get the diameter of one of the balls, we can get the radius first and multiply the value by 2 since the diameter is 2 times the radius length
A ball is spherical in shape
The volume of a sphere is:
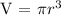
Thus:
![\begin{gathered} r^3=(37.1)/(\pi)^{}^{}^{} \\ \\ r\text{ = }\sqrt[3]{(37.1)/(\pi)} \\ \\ r\text{ = 2.277 in} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/lcidtip51acrbxzeqanz3lw177ue6d8pgb.png)
To get the diameter, we simply multiply this by 2