For the badminton players, there are 4 available and the committee will choose 3, so the number of possible ways of choosing is a combination of 4 choose 3.
A combination of n choose p is given by:
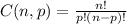
So, for n = 4 and p = 3, we have:
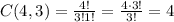
For the volleyball players, the committee will choose 2 from 5, so we have:
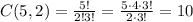
Now, for the basketball players, the committee will choose 1 from 2, so we have:
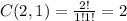
Multiplying all the number of possible ways of each type of player, we have the number of different committees:
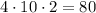
Therefore there are 80 different committees that can be formed.