ANSWER
Option B
Step-by-step explanation
We want to find the expression that is equivalent to:
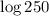
To do this, we have to express 250 as an exponent of 10.
That is:
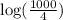
Now, we can separate the terms using one of the laws of logarithm that states that:
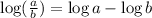
Therefore, we have that:
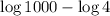
Now, simplifying further, we have:
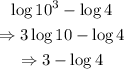
The answer is option B.