Question

Find the angle between the following two lines: 2x + y = 4x − y = 2 (round your answer to the nearest tenth of a degree).

Answer 1

We are given the lines

`2x+y=4`

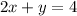
and

`x-y=2`

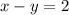
So, if the slope of the first line is m1 and the slope of the second line is m2, then the angle theta between both lines can be described by

`\tan (\theta)=\pm((m_2-m_1))/((1+m_1\cdot m_2))`

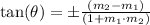
So, to define the angle theta, we need to find the slope of each line. To do so, we will express each equation into its slope intercept form. Recall that the slope intercept form of the line equation would be

`y=mx+b`

where m is the slope and b is the y intercept.

For the first line, if we subtract 2x on both sides, we get

`y=-2x+4`

For the second line, if we add y on both sides and then subtract 2 on both sides, we get

`y=x-2`

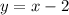
This means that the slope of the first line is m1=-2 and the slope of the second line is m2=1. So, if we replace this values in the formula, we get

`\text{tan(}\theta)=\pm(((1)-(-2)))/((1+1\cdot(-2))=\pm(1+2)/(1-2)=\pm(3)/(-1)=\pm3`

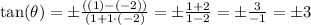
So, applying the arctan function on both sides, we get

`\theta=\tan ^(-1)(\pm3)=71.56505\approx71.6`

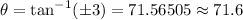
So the measure of the angle between both lines is about 71.6°