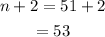Question

There are 3 consecutive integers that have a sum of 156. What is the value of the greatestinteger?

Answer 1

53

Step-by-step explanation:

Let the first integer = n

• The second consecutive integer = n+1

,

• The third consecutive integer = n+2

If the sum of the integers is 156, then:

`n+(n+1)+(n+2)=156`

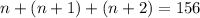
Solve for n.

`\begin{gathered} n+n+n+1+2=156 \\ 3n+3=156 \\ 3n=156-3 \\ 3n=153 \\ n=(153)/(3) \\ n=51 \end{gathered}`

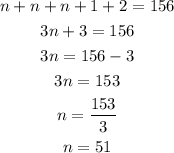
Thus, the value of the greatest consecutive integer will be:

`\begin{gathered} n+2=51+2 \\ =53 \end{gathered}`