SOLUTION
Write the equations
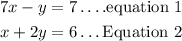
Using substitution method
Make x the subject of formula from equation 2
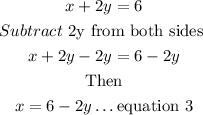
Substitute the expression for x in equation 3 into equation 1

Then, divide both sides by -15 to obtain the value of
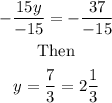
Finally, substitute the value of y into equation 3 to obtain x
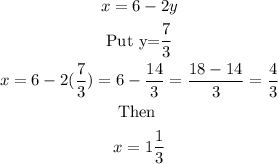
Therefore
Answer: x=1 1/3 and y=2 1/3
Option C