Hello could you help me solve this question? (9.11 Solving Logarithmic Equations #14)

Question

asked Jun 13, 2023 61.4k views

1 Answer

Alex Pilugin · Answer 1 · 2023-06-19T16:35:54+0000

Answer

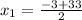
Step-by-step explanation

Given

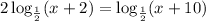
$2\log_{(1)/(2)}(x+2)=\log_{(1)/(2)}(x+10)$

We can use the logarithmic properties to simplify our equation, where:

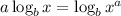
$a\log_bx=\log_bx^a$

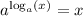
$a^(\log_a(x))=x$

Applying this rule to both sides of our problem given:

$(1)/(2)^{\operatorname{\log}_{(1)/(2)}(x+2)2}=(1)/(2)^{\operatorname{\log}_{(1)/(2)}(x+10)}$
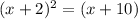
(x+2)^2=(x+10)

Solving the squared expression:

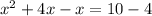
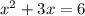
Setting the equation to 0:

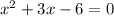
Using a scientific calculator to get the result:

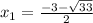
If we verify the solutions the correct one is the first.