Answer: 3/4 ( Option D )
Explanations:
The given expression is:
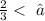
To know which fraction will go into the blank, we consider the options one by one, and which ever is true is the correct choice.
Find the LCM so that both fractions have a common denominator and see if what happens at the numerator is true
Option A is 1/8, therefore lets see if 2/3 is truly less that 1/8

Option B is 3/6. Let us see if 2/3 is truly less than 3/6

Option C is 3/5. Let us see if 2/3 is truly less than 3/5

Option C is 3/4. Let us see if 2/3 is truly less than 3/4

2/3 < 3/4 is the correct expression. Therefore, option D is the right choice