Question

1.Use conservation of angular momentum to solve the problem. You sit on a chair with both arms stretched out. At this position you are spinning with an angular velocity of 10 units and you have a rotational inertia of 20units.After certain time you moved your hands back to your chest and in this position your rotational inertia is 10units.What would be your new speed of rotation?

Answer 1

Given:

The angular velocity is

`\omega_1=\text{ 10 units}`

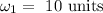
The rotational inertia is

`I_1=\text{ 20 units}`

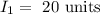
To find the angular speed when rotational inertia is

`I_2=\text{ 10 units}`

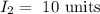
Step-by-step explanation:

According to the conservation of angular momentum,

`I_1\omega_1=I_2\omega_2`

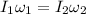
The angular speed can be calculated as

`\begin{gathered} \omega_2=(I_1\omega_1)/(I_2) \\ =(20*10)/(10) \\ =20\text{ units} \end{gathered}`

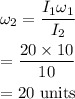
Thus, the angular speed is 20 units when the rotational inertia is 10 units.