Answer:
Let the price for one $1 increase be
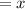
Let the revenue be represented as
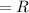
The number of tickets sold will be represented below as

The price per ticket will be represented below as
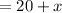
The revenue is calculated using the formula below
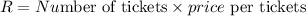
By substituting the values above, we will have
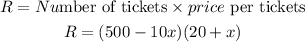
Expanding the brackets, we will have

Step 1;
We would calculate the value of x that will give maximum revenue
We will use the expression below

The general form of a quadratic equation is given below as
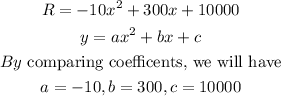
By substituting the values, we will have
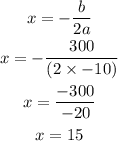
Therefore,
The price per ticket that will maximize profit will be
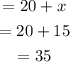
Hence,
The price per ticket that will maximize profit will be = $35
Step 2:
To calculate the maximum revenue, we will substitute the value of x= 15 in the equation for the revenue given below
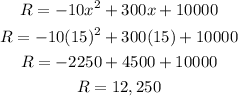
Hence,
The maximum revenue is = $12,250