Answer:
3 seconds
Step-by-step explanation:
The initial velocity is 60 m/s at an angle of 30° to the horizontal, so we can calculate the initial velocity in the vertical direction as
Viy = Vi sin(θ)
Viy = 60 sin(30)
Viy = 60(0.5)
Viy = 30 m/s
Then, we can use the following equation to calculate the time that it takes to reach the maximum height.
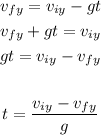
At a maximum height the vertical velocity is 0 m/s, so replacing viy = 30 m/s, vfy = 0 m/s and g = 10 m/s², we get

Therefore, the answer is 3 seconds