Question

I really need help with this can u please explain how to do it

Answer 1

Solving by substitution method.

If we clear y in equation 1, we get:

`y=3+x`

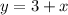
Now, if we substitute this result into equation 2, we have

`3x+(3+x)=-1`

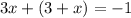
By clearing parenthesis, we get 3x+3+x=-1.

Now, by combining similar terms, we obtain

`4x+3=-1`

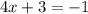
If we move +3 to the right hand side as -3, we have

`\begin{gathered} 4x=-1-3 \\ 4x=-4 \\ x=-(4)/(4) \\ x=-1 \end{gathered}`

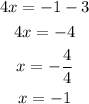
Finally, by substituting this result into out first equation, we get

`\begin{gathered} y=3+(-1) \\ y=3-1 \\ y=2 \end{gathered}`

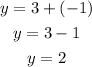
Therefore, the solution of the system is x=-1 and y=2.