ANSWER
1488.07 in³
Step-by-step explanation
This shape is formed by two standard shapes: a cone and a half-sphere.
The volume of a cone is,
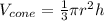
Where r is the radius of the base and h is the height of the cone.
The volume of a sphere is,
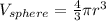
Where r is the radius of the sphere.
In this case, for both the sphere and the cone, the radius is r = 7 inches, and the height of the cone is h = 15 inches. The total volume of the shape is the sum of the volume of the cone and half the volume of the sphere,
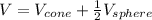
Let's find the volume of the cone and the sphere,
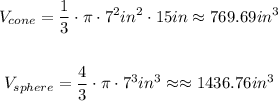
So the total volume is,
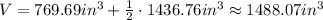
Hence, the volume of the entire shape is 1488.07 cubic inches.