Let P be the cost of a box of pretzels and C be the cost of a bag of candy.
The cost of 4 boxes of pretzels is 4P, and the cost of 6 bags of candy is 6C. Since Angela sold 4 boxes of pretzels and 6 bags of candy, raising $108, then:
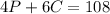
Similarly, from Kevin's information we can conclude that:
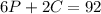
These two equations lead to a 2x2 system of equations. To solve it, isolate C from the second equation:
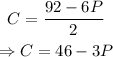
Then, substitute the expression for C into the first equation:

Solve this equation for P:
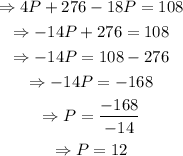
Substitute P=12 into the expression for C to find its value:
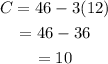
Therefore, a box of pretzels is worth $12 and a bag of candy is worth $10.