Question

What is the end behavior ?Is the degree even or odd ?What is the local maxima ?What is the local minima ?Identify the real zeros ?What is the domain ? What is the range ?

Answer 1

From the given figure

We have a curve that decreases on the left part until getting the minimum vertex (-2, 0), then increases until getting the maximum point (2, 4), then decreasing again

The local minimum is (-2, 0) the minimum value is 0

The local maximum is (2, 4) the maximum value is 4

The zeroes of the graph are the point of intersection between the curve and the x-axis

Since the curve intersects the x-axis at points (-2, 0) and (4, 0), then

The roots are -2 and 4

The domain is the values of x

Since the graph moves from left - infinity to right infinity, then the domain is

`D=\rbrack-\infty,\infty\lbrack`

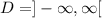
The range is the values of y corresponding to x

Since the graph moves up and down from - infinity to infinity, then

`R=\rbrack-\infty,\infty\lbrack`

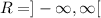
Let us find its end behavior

Since the part of the left side is decreasing and the part of the right side is also decreasing, then

The behavior is

`\begin{gathered} x\rightarrow-\infty,f(x)\rightarrow\infty \\ x\rightarrow\infty,f(x)\rightarrow-\infty \end{gathered}`

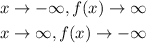
The degree of the function is odd because the greatest power for this graph is 3