Answer:
8 years.
Explanation:
• The initial value of the laptop computer = $4700
,
• Growth/Decay Rate = 75%=0.75
Thus, the value of the laptop after t years will be:
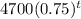
When the laptop is worth $600 or less:
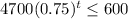
We solve for t:
![\begin{gathered} \text{Divide both sides by 4700} \\ (4700(0.75)^t)/(4700)=(600)/(4700) \\ (0.75)^t=(600)/(4,700) \\ \text{ Take the log:} \\ \log(0.75)^t=\log((600)/(4,700)) \\ \text{ By the power law of logarithm:} \\ t\log(0.75)=\log((6)/(47)) \\ \text{ Divide both sides by log 0.75} \\ t=\frac{\operatorname{\log}((6)/(47))}{\operatorname{\log}(0.75)} \\ t=7.12 \end{gathered}]()
Thus, the computer be worth $600 or less after 8 years.