11. The exponential function that models the growth is as follows:
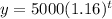
Where t is the time in hours. In this case, if we double the population we have to:
y = 5000 x 2 = 10000
Therefore, substitute y = 10000 in the function and solve for t:
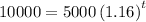
Divide both sides by 5000:
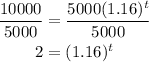
Apply the laws of exponents:
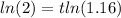
Solve for t:
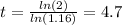
Answer: B. 4.7 hours