We have that the vertex form of the equation of the parabola is:
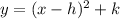
where (h,k) is the vertex. Tipically, the minimum of the parabolla is located at the vertex if the parabola is positive. In this case, if the parabolla reaches its minimum value at (-2,-3), then, the equation in vertex form is:
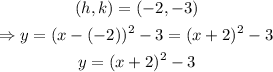
therefore, the required equation is y = (x+2)^2 - 3