Solution:
Given:
Let d represent the number of dimes coins.
Let n represent the number of nickels coins.
Recall:
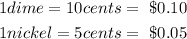
To generate the system of equations:
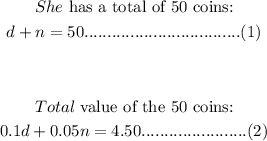
From equation (1);
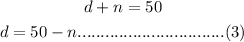
Substitute equation (3) into equation (2);

Substitute the value of n into equation (3);
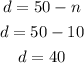
Therefore, Daphne has 40 dimes coins and 10 nickels coins.