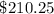Given that Danielle deposits $200 into a bank account that compounds interest at a monthly rate of 1%;
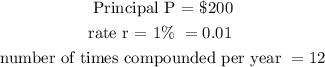
If Danielle leaves her money in the bank for 5 years;
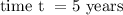
Recall that the formula for compound interest is;
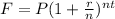
where F is the final value;
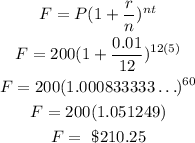
Therefore, the amount she will have is;