Question

A ball is suspended from two cords as illustrated belowA) determine the magnitude of the tension in the angled cordB) what is the magnitude of the tension in the vertical cord attached to the ballC) calculate the mass of ball

Answer 1

a)

Since the ball is in equilibrium, the sum of horizontal forces are equal zero.

We can decompose the tension in the angled cord in horizontal and vertical components, and then calculate the sum of horizontal forces in the diagram:

`\begin{gathered} T_(2x)=T_2\cdot\cos (57\degree) \\ T_(2x)=T_2\cdot0.545 \\ \\ T=T_(2x) \\ 250=T_2\cdot0.545 \\ T_2=(250)/(0.545) \\ T_2=458.7\text{ N} \end{gathered}`

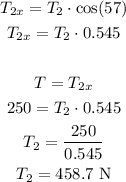
So the tension in the angled cord is 458.7 N

b)

To find the tension in the vertical cord, we can find the vertical component of the tension in the angled cord, since these two forces are equal because the ball is at equilibrium:

`\begin{gathered} T_(2y)=T_2\cdot\sin (57\degree) \\ T_(2y)=458.7\cdot0.839 \\ T_(2y)=384.85\text{ N} \\ \\ W=T_(2y) \\ W=384.85\text{ N} \end{gathered}`

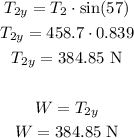
So the tension in the vertical cord is 384.85 N

c)

To calculate the mass of the ball, let's use the weight formula:

`\begin{gathered} W=m\cdot g \\ 384.85=m\cdot9.8 \\ m=(384.85)/(9.8) \\ m=39.27\text{ kg} \end{gathered}`

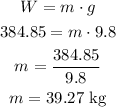
So the mass of the ball is 39.27 kg