EXPLANATION :
From the problem, we have the points :
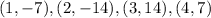
The points represent an exponential function if all points satisfy the equation in the form :

Let's try (1, -7)

(2, -14)
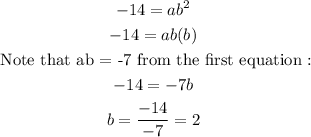
We have b = 2.
Using the first equation, solve for a :
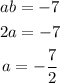
So the equation now will be :
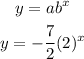
Let's check the third and fourth points, they must satisfy the equation :
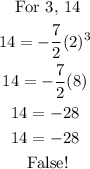
Since the third point does NOT satisfy the equation, therefore, this is NOT an exponential function