Dominic is driving on a long road trip. He currently has 10 gallons of gas in his
car. Each hour that he drives, his car uses up 1.25 gallons of gas. Write an
equation to represent the scenario. How much gas will Dominic have in 3
hours?
Step 1
Let
Dominic has 10 gallons of gas
. Each hour that he drives, his car uses up 1.25 gallons of gas, here we have a relation between the time and the gas the car uses
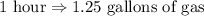
Write an
equation to represent the scenario
Step 2
use a rule of three
Let
y, the gas the car uses
x, the time Dominic drives
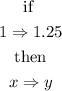
the relation is
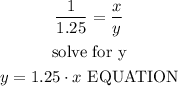
Step 2
How much gas will Dominic have in 3
hours?
find y when x=3, this is the gas use
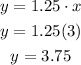
Step 3
the gas Dominic has is
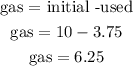
Then, after 3 hours Dominic has 6.25 gallons