Consider the given rational function,
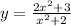
Consider that the function will become indeterminate, if the denominator becomes zero.
This point at which the function takes the indeterminate form will be the point of discontinuiity for the rational function,
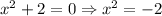
Note that this is not possible for any real number i.e. the square of a real number cannot be negative.
It means that the expression in the denominator cannot be zero for any real number 'x'.
Thus, we can conclude that the given rational function has no point of discontinuity.